Overview

• Kingma, Diederik P. and Ba, Jimmy. Adam: A method for stochastic optimization. ICLR, 2014.
• Adaptive Moment Estimation 의 약자
• Optimizer 중 가장 좋다고 알려져 있고, deep network 일수록 Adam이 좋다고 한다
• 각 패러미터에 대한 adaptive learning rate를 설정한다
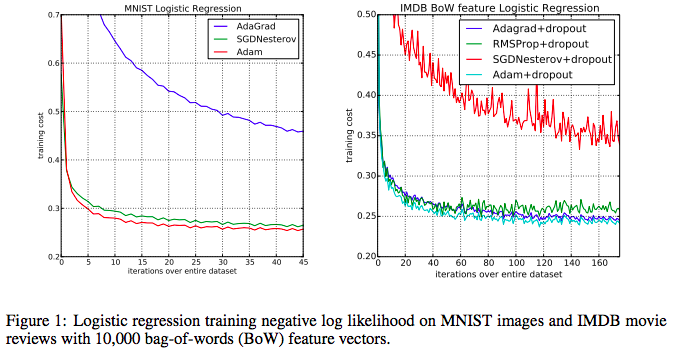
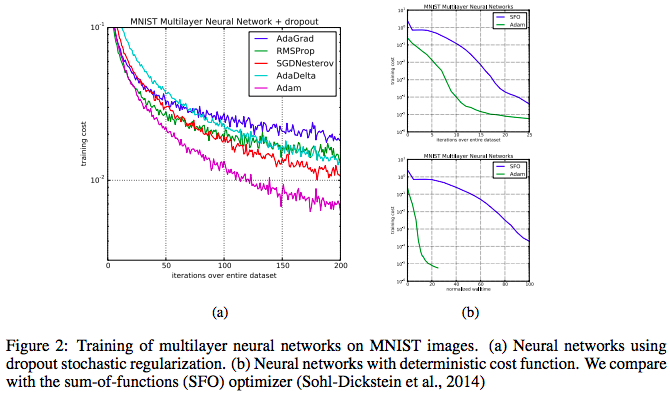
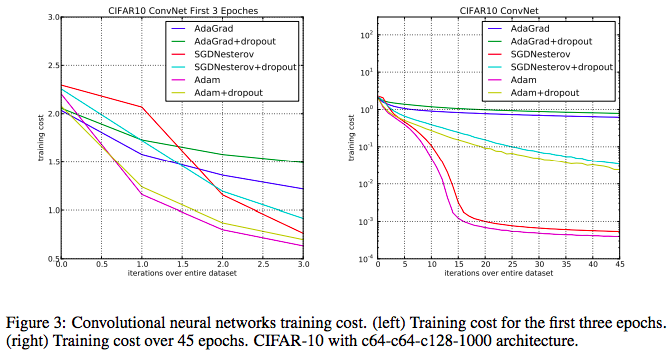
• Tensorflow MNIST 튜토리얼에서 softmax classifier를 사용하면 91% 정확도의 모델을 구축 가능하나, 동일한 환경에서 Adam optimizer로 바꿀 경우 96% 정확도의 모델을 얻을 수 있다
• AdaGrad(works well with sparse gradients)와 RMSProp(works well in non-staionary settings) 의 장점을 합침
• gradient와 그것의 제곱인 magnitude의 exponentially decaying (moving) average를 취하고 parameter update에 사용한다

Kingma & Ba, 2014

Pseudo-code from Tensorflow docs

Construct a new Adam optimizer.
Initialization:

m_0 <- 0 (Initialize initial 1st moment vector)  
v_0 <- 0 (Initialize initial 2nd moment vector)  
t <- 0 (Initialize timestep)  

The update rule for variable with gradient g uses an optimization described at the end of section2 of the paper:

t <- t + 1  
lr_t <- learning_rate * sqrt(1 - beta2^t) / (1 - beta1^t)  
 
m_t <- beta1 * m_{t-1} + (1 - beta1) * g.  
v_t <- beta2 * v_{t-1} + (1 - beta2) * g * g  
variable <- variable - lr_t * m_t / (sqrt(v_t) + epsilon)  

The default value of 1e-8 for epsilon might not be a good default in general.
For example, when training an Inception network on ImageNet a current good choice is 1.0 or 0.1.
Note that in dense implement of this algorithm, m_t, v_t and variable will update even if g is zero, but in sparse implement, m_t, v_t and variable will not update in iterations g is zero.

Alec Radford’s animations for

optimization algorithms (unfortunately no Adam…)

• “Noisy moons: This is logistic regression on noisy moons dataset from sklearn which shows the smoothing effects of momentum based techniques (which also results in over shooting and correction). The error surface is visualized as an average over the whole dataset empirically, but the trajectories show the dynamics of minibatches on noisy data. The bottom chart is an accuracy plot.”

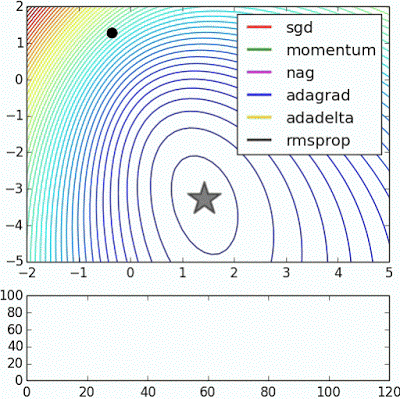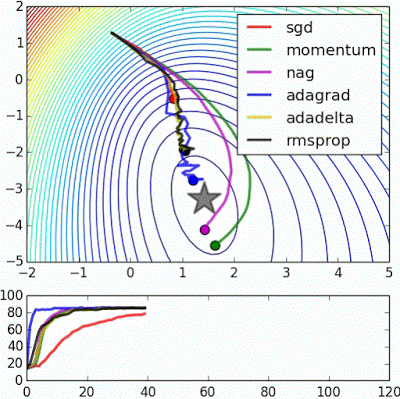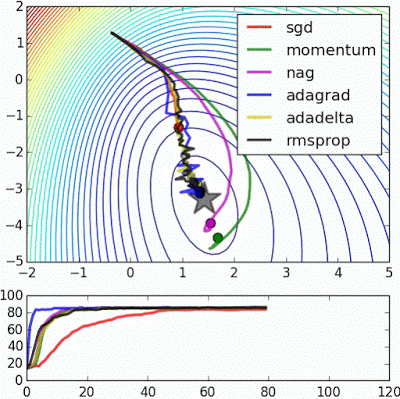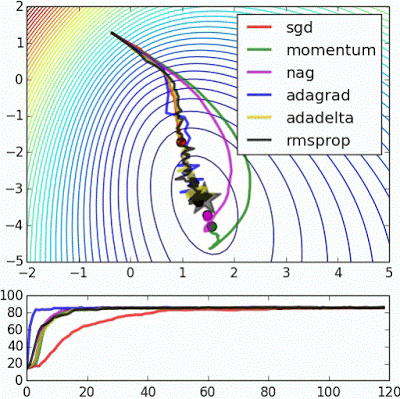
• “Beale’s function: Due to the large initial gradient, velocity based techniques shoot off and bounce around - adagrad almost goes unstable for the same reason. Algos that scale gradients/step sizes like adadelta and RMSProp proceed more like accelerated SGD and handle large gradients with more stability.”

• “Long valley: Algos without scaling based on gradient information really struggle to break symmetry here - SGD gets no where and Nesterov Accelerated Gradient / Momentum exhibits oscillations until they build up velocity in the optimization direction. Algos that scale step size based on the gradient quickly break symmetry and begin descent.”

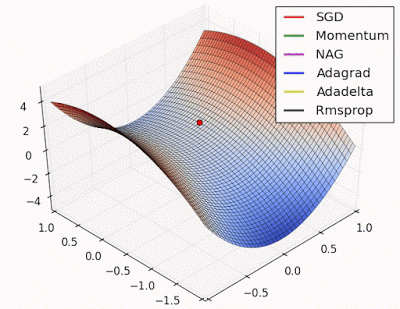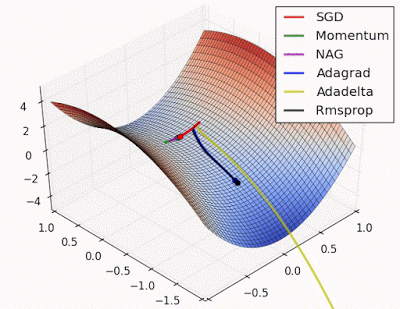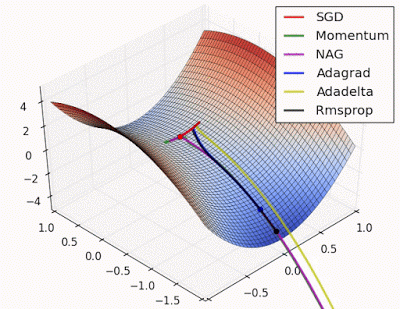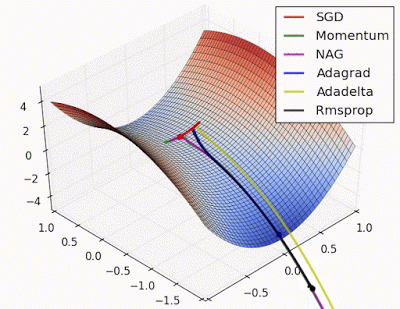
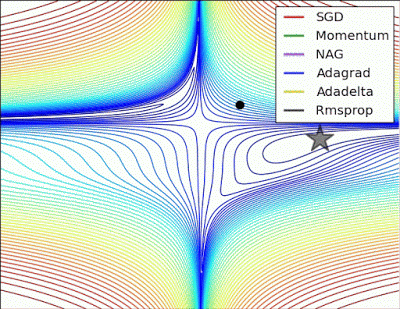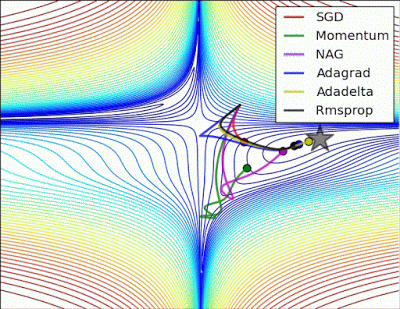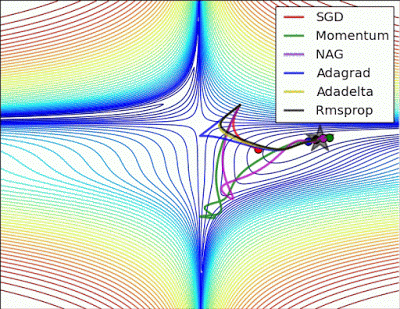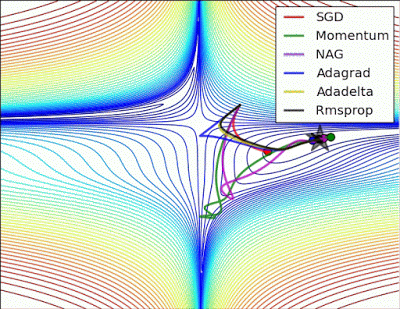
• “Saddle point: Behavior around a saddle point. NAG/Momentum again like to explore around, almost taking a different path. Adadelta/Adagrad/RMSProp proceed like accelerated SGD.”

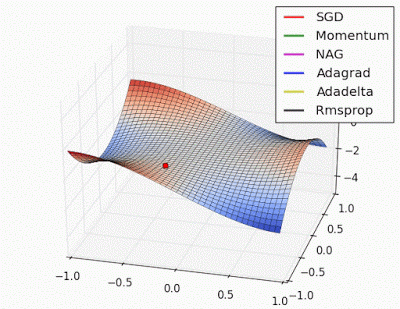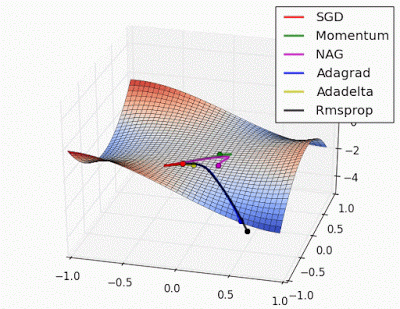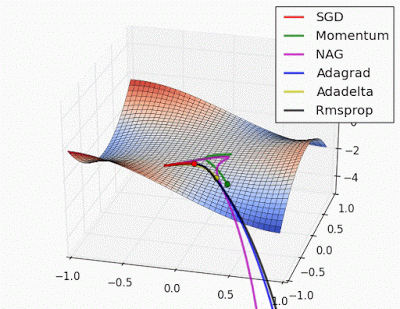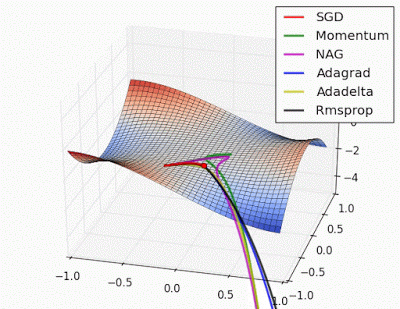
More on Optimization algorithms:

An overview of gradient descent optimization algorithms

Sung Hah Hwang